Light Part 3

How to Use Light to Cool and Trap Atoms, Part 3: Trapping Atoms with Light (MOTs)

By Jared Popowski

2023-02-05

This is the final part in our series on cooling and trapping atoms with light! Today we are describing how atoms can be trapped with the use of light. Like last time, we will only focus on a single method for trapping atoms, the magneto-optical trap (MOT). Figure 1 below is a simplified diagram of a MOT. As the name suggests, MOTs trap atoms by combining the ideas of how magnetic fields can be used to split energy levels in atoms (magneto), and how light can be used to cool atoms (optical) [1]. Our job in this post is mainly to talk about the purpose of the magnetic field in the trap, because we already learned most of what we need to know for the optical part in the last post about Doppler cooling! To quickly summarize that post, moving atoms experience a Doppler shift in the frequency of the light that hits them, and for well-chosen laser frequencies this Doppler shift will hit an atomic resonance, at which point the light’s energy is absorbed by the atom and momentum conservation means that the atom experiences a kick against its motion by the light. In this way, atoms are cooled down with light. But how is this combined with a magnetic field to create a MOT?

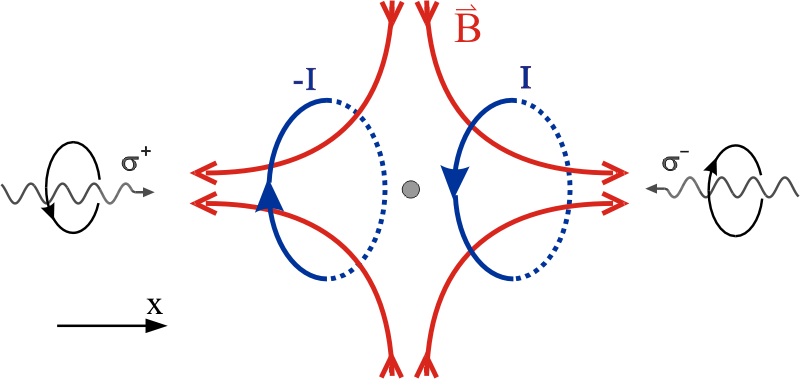Figure 1: A simplified diagram of a MOT. Counterpropagating laser beams (on far left and right sides) provide the laser cooling part of the trap, and two magnetic field coils with current running through them in opposite directions (called an Anti-Helmholtz coil configuration) provide the magnetic field that (together with the lasers), forces atoms to the center of the trap. Image from Wikimedia Commons.

To answer this question, we must first answer the question “What effect does a magnetic field have on atoms?” The short answer is “It depends.” The response of an atom to a magnetic field depends on the atom’s magnetic dipole moment. The magnetic dipole moment is a vector quantity that tells you how strongly the object will try to rotate and align itself with an externally applied magnetic field, and any object that creates magnetic fields has an associated magnetic dipole moment. Think of a bar magnet with a North and South Pole. If you try to touch this magnet with another one that is aligned in the opposite direction (i.e. aligned like N-S S-N), then the second magnet will resist and try very hard to rotate and align itself with the field of the first magnet. But if we instead bring a wood block up to the first magnet, it won’t resist us touching the other magnet at all. This is due to the magnet having a vastly larger net magnetic dipole moment than a block of wood.

Protons, neutrons, and electrons, the constituent particles of atoms, also have intrinsic magnetic dipole moments, associated with the quantum mechanical spins of the particles. The total magnetic moment of an atom is the vector sum of these constituent magnetic moments. The key point for MOTs is that an atom with a nonzero total magnetic moment will have quantum states that increase in energy with increasing magnetic field and states that decrease in energy, depending on the orientation of the atom’s magnetic moment with the external magnetic field of the MOT [2]. This property of atoms with magnetic moments is called the Zeeman effect, and is depicted in Figure 2 below.

Figure 2: A diagram of the Zeeman effect. In a nonzero magnetic field, the energy level of the atom splits based on the different orientations of the atom’s magnetic moment with respect to the external field. Image from Wikimedia Commons.

In a MOT, a pair of magnetic coils with equal current running in opposite directions creates a magnetic field pattern that has a minimum in the center of the trap, and then increases in strength linearly with the distance from the center (red arrows in Figure 1). This means that atoms in the middle will experience no Zeeman splitting of its energy levels, while atoms displaced from the center will have Zeeman splitting, like in Figure 2 above. Now we load a sample of atoms in between the magnetic coils and apply laser beams that are traveling in opposite directions, with a frequency (and thus energy) that is slightly lower than the resonant frequency of the atoms in the center of the trap. See Figure 3 below for a one-dimensional model of this situation. The symmetric Zeeman splitting on both sides of the trap center means that at a certain distance from the center, our laser will become on-resonance with one of our atom’s split energy states, where it is then absorbed by the atom (vertical arrows in Figure 3). This causes the atom to feel a momentum kick back towards the center of the trap. Note that this laser setup is the same that we use for Doppler cooling, which we talked about in the last blog post! So fast-moving atoms in our trap will also experience a Doppler shift in the laser frequency that cools down our atoms. And that’s it, we have a MOT! Now we can hold a collection of atoms by continually forcing them back into the center of our trap with a magnetic field and cooling them down with light. There is a final nuance in that we must choose the lasers to have opposite circular polarization, so that the atom will only be excited to the specific energy levels shown in Figure 3 (m = +1 on the left, m = -1 on the right), but I do not want to dive too far down the rabbit hole by explaining polarization in this post.

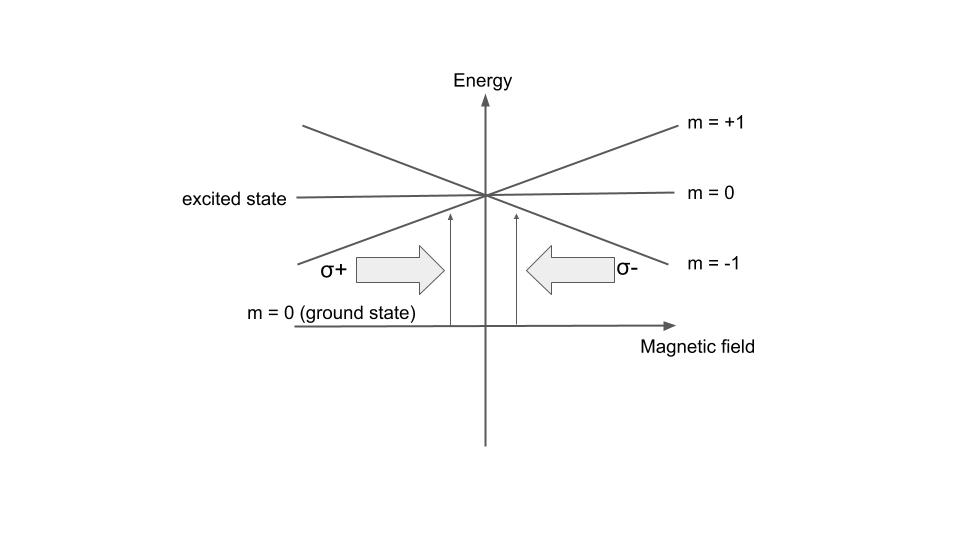Figure 3: A one-dimensional model of the principles behind a MOT. The magnetic field linearly increases with distance, meaning that the Zeeman splitting of the atom’s excited state also increases with distance. At a certain distance from the center of the trap, opposing circularly polarized laser beams enter resonance with the atom’s ground state to excited state transition. This causes the atom to absorb the energy of a photon from the laser, feeling a momentum kick back towards the center of the trap in the process. Image inspired by [3].

I began this series by talking about what light actually is. The idea was partially to get us comfortable with the habit of switching back and forth between the ideas of light as a wave and light as a particle whenever convenient, but I also hoped to get across a sense of the versatility of light. In experiments, light can be the object of interest, the measurement device, or a useful tool. That’s what this whole series is about, and that’s what got me interested in communicating these ideas in the first place. Before I started working in an atomic physics laboratory, I had this idea in my head that lasers are somehow inherently hot. When I first learned that lasers were used to cool down and trap atoms, I was amazed! Honestly, it still amazes me. I hope that some of this amazement came across in the series.

As always, feel free to comment any feedback you have about this post, or suggestions for future topics for this blog. Also, if you want to get an email every time I release a new blog, make sure to sign up for email updates below!

References

[1] Bergeson, Scott. Physics 571 Lecture #31. Fall 2009. PDF. https://www.physics.byu.edu/faculty/bergeson/physics571/old/lecturenotes/mot.pdf

[2] Phillips, W. D. “Laser cooling and trapping of neutral atoms.” USPEKHI FIZICHESKIKH NAUK 169.3 (1999): 305-322. https://www.nobelprize.org/uploads/2018/06/phillips-lecture.pdf

[3] Sproles, David E. Laser spectroscopy and magneto-optical trapping of rubidium atoms. Diss. The Graduate School, Stony Brook University: Stony Brook, NY., 2008.